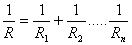|
1.Същност
2.Последователно свързване
3.Успоредно свързване
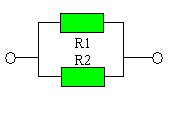
Сега ще споменем и успоредното (също се нарича паралелно свързване). На картинката вляво има схема на този вид свързване. Отново два резистора, точно като по-горе, но този път успоредно свързани. Отново ще им зададен някакво съпротивление, но този път за да е по-лесно единият ще бъде примерно 4 ома, а другият - 6 ома. При паралелното свързване обаче еквивалентното съпротивление не се изчислява толкова лесно. За два резистора, обаче има една опростена формула - R = (R1 * R2) / (R1 + R2). Тоест в нашият случай еквивалентното съпротивление R е равно на (4 * 6) / (4 + 6) = 24 / 10 - 2,4 ома. Това не е особено трудно за пресмятане, но не бива да забравяме, че в нашият случай говорим само за два резистора - я си представете примерно 10 такива свързани паралелно - за такива случай има една универсална формула :
Тя може да изглежда малко сложна, но в действителност не е точно така. Ще вземем три резистора - един 6, един 4 и един 3 ома. Нека изчислим - 1/R = 1/6 + 1/4 + 1/3 . Сега трябва да приведем под общо знаменател - не сме в 5-ти клас, за да обяснявам това, но в този случай най-малкото общо кратно е 12. Като умножим всички дроби по него се получава - 1/R = 2/12 + 3/12 + 4/12 или 1/R = 9/12. Резултата е - R = 12/9 = 1.33 ома. Това е. 4.Смесено свързване До тук добре. Разучихме двата вида свързване на консуматори. Но има един трети - всъщност той не е точно деклариран, а просто се отнася за всички други случаи с 3 или повече консуматора - резистора, в които не може да се определи точно едното или другото свързване. То се нарича смесено - ето един пример :
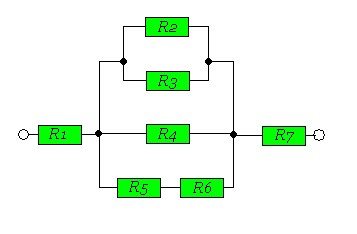
Тук имаме 7 резистора свързани по всевъзможен начин. Това е един типичен пример за смесено свързване. Сигурно се чудите точно как да се изчисли еквивалентното съпротивление на толкова много консуматори свързани по безразборен начин. Ето как - просто ги групираме в по-малки вериги, по два, за да си създадем представа за цялата верига. Примерно веднага може да се забележи, че R2 и R3 са свързани паралелно - изчисляваме за тях. След това - R5 и R6 - са последователно - изчисляваме и за тях. Сега след като имаме за двете групи - R2, R3 и R5, R6 еквивалентни съпротивления можем с тях да изчислим това за цялата средна част, като изчислим тези две групи и R4 със формулата за паралелно свързване. Сега имаме за R2, R3, R4, R5 и R6 едно съпротивление - накрая трябва просто да ги съберем с това на R1 и R7, тъй като средната част е последователно свързана с тях и - готово. Вече имаме за цялата система. |
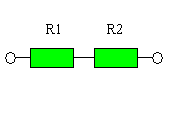 Последователно
свързване имаме, когато консуматорите са свързани един след друг (в
низ) във веригата. Пример за такъв вид свързване е даден на
картинката вляво. На нея имаме два резистора, които са свързани
последователно. Те са
Последователно
свързване имаме, когато консуматорите са свързани един след друг (в
низ) във веригата. Пример за такъв вид свързване е даден на
картинката вляво. На нея имаме два резистора, които са свързани
последователно. Те са